2025/12/22
In MOSFET switching, the gate driver plays a critical role in charging and discharging the gate, and the underlying energy conversion process directly affects the efficiency and thermal design of the driver system. Although the conventional power loss equations are widely used, they can lead to misunderstandings in certain applications. This article re-examines the actual energy flow in driver circuits by analyzing several typical charging/discharging models, and further discusses the impact of parasitic inductance on system energy conservation, providing engineers with a more accurate basis for energy estimation and device selection.
1.Common Power Loss Calculation Equations for Driver Circuits
The driver charges the MOSFET as shown in Figure 1, and discharges it as shown in Figure 2:
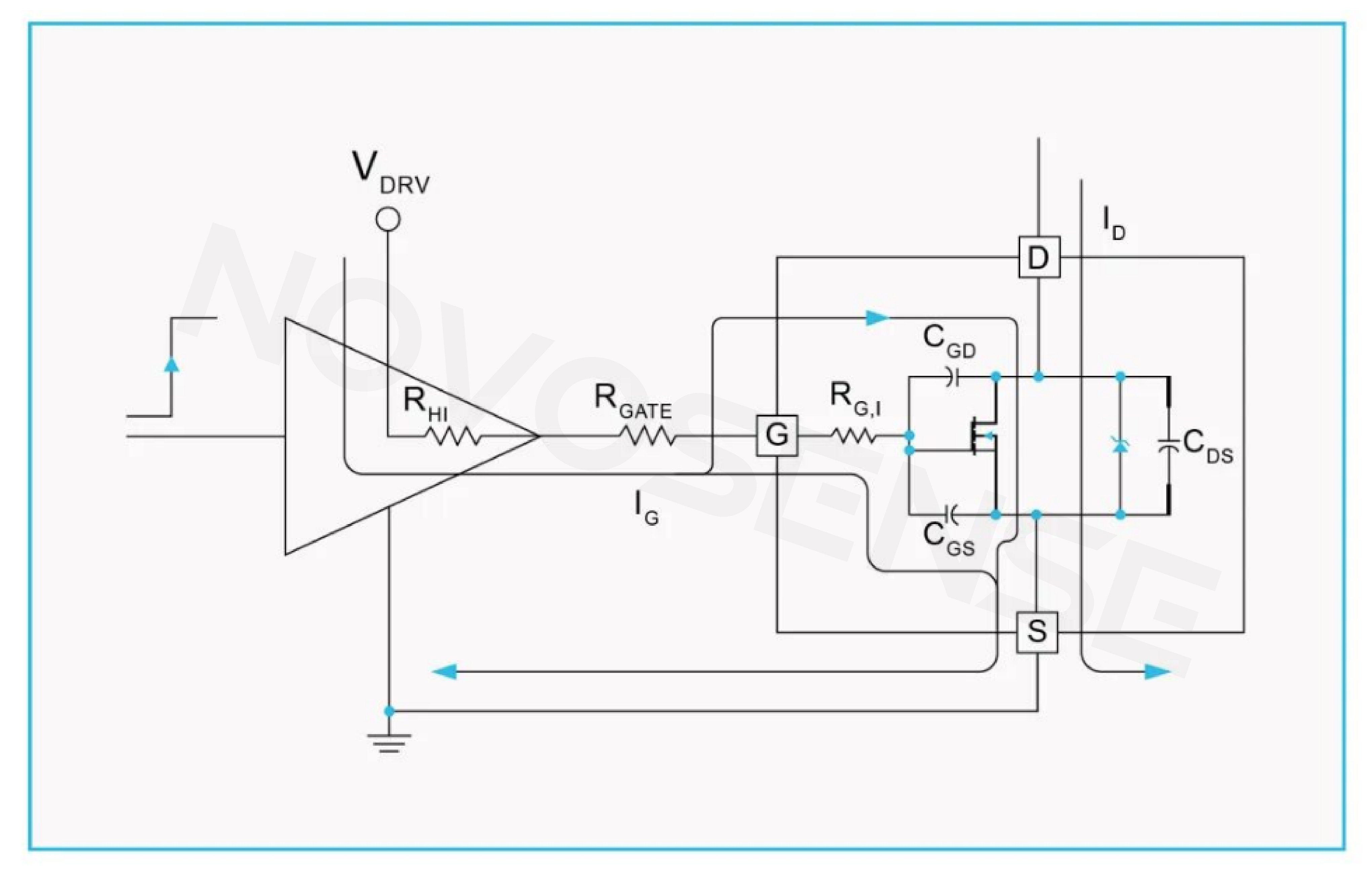
Figure 1: Charging
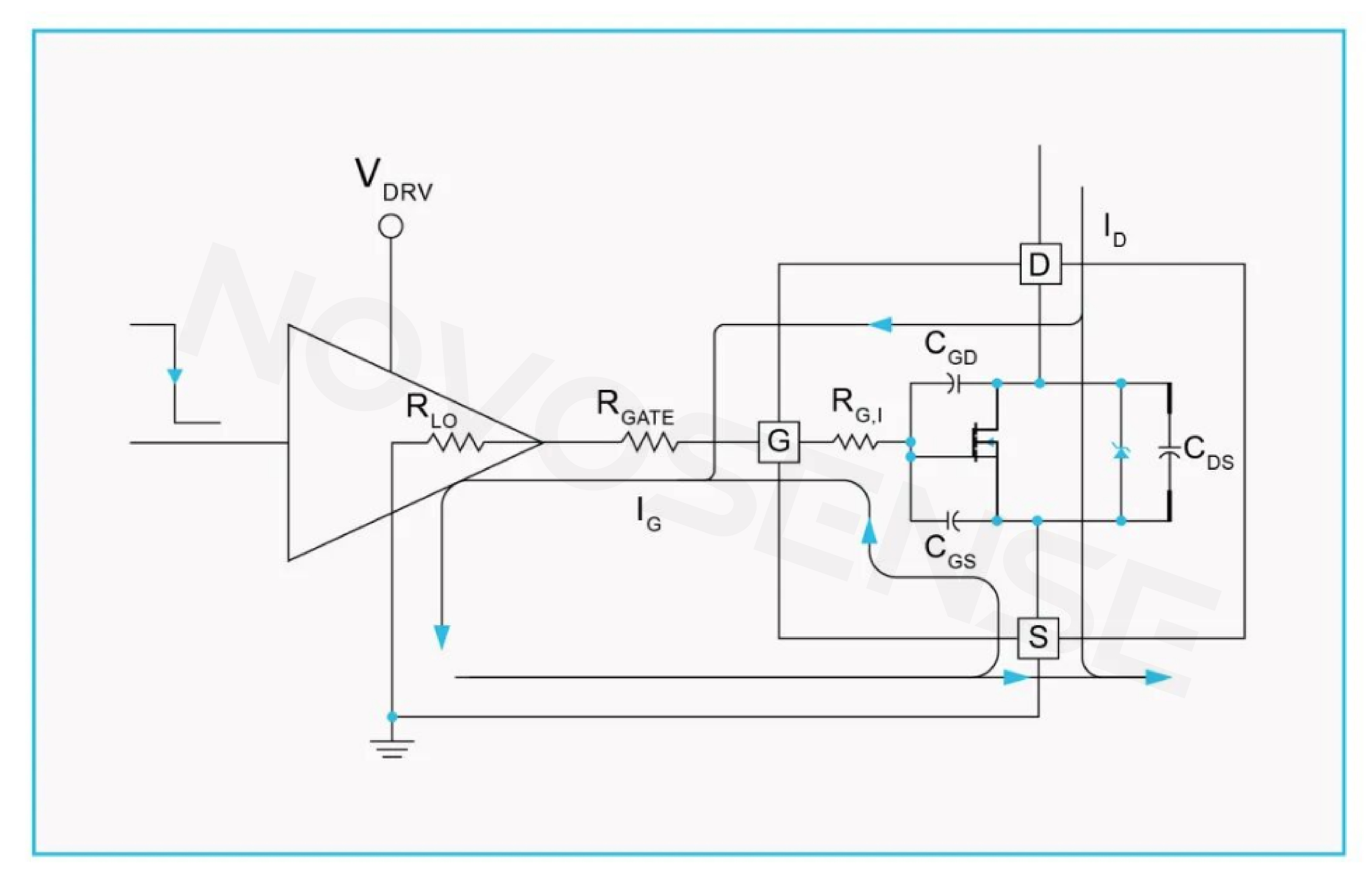
Figure 2: Discharging
The power loss is calculated using the following equations:
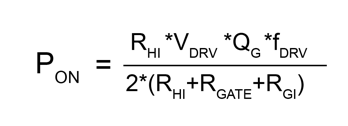……（1）
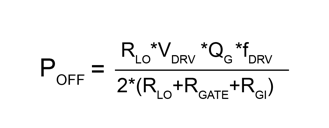……（2）
Where:
QG is total gate charge at the end of charging.
fDRV is gate drive frequency.
VDRV is drive voltage.
QG*fDRV represents the average charging current.
VDRV*QG*fDRV represents the average power supplied by the source.
Equations (1) and (2) divide this power equally: half dissipated in the resistors and half stored in the capacitor. During discharge, the energy stored in the capacitor is dissipated through the resistor.
Clearly, the condition for equations (1) and (2) to hold is that the energy dissipated in the resistor equals the energy stored in the capacitor during charging. However, is this assumption always valid? Obviously not when the resistance is zero. What about when resistance is non-zero?
2. Constant Voltage Source Charging a MOSFET
The MOSFET charging waveform is shown in Figure 3, and the I-V curve in Figure 4.
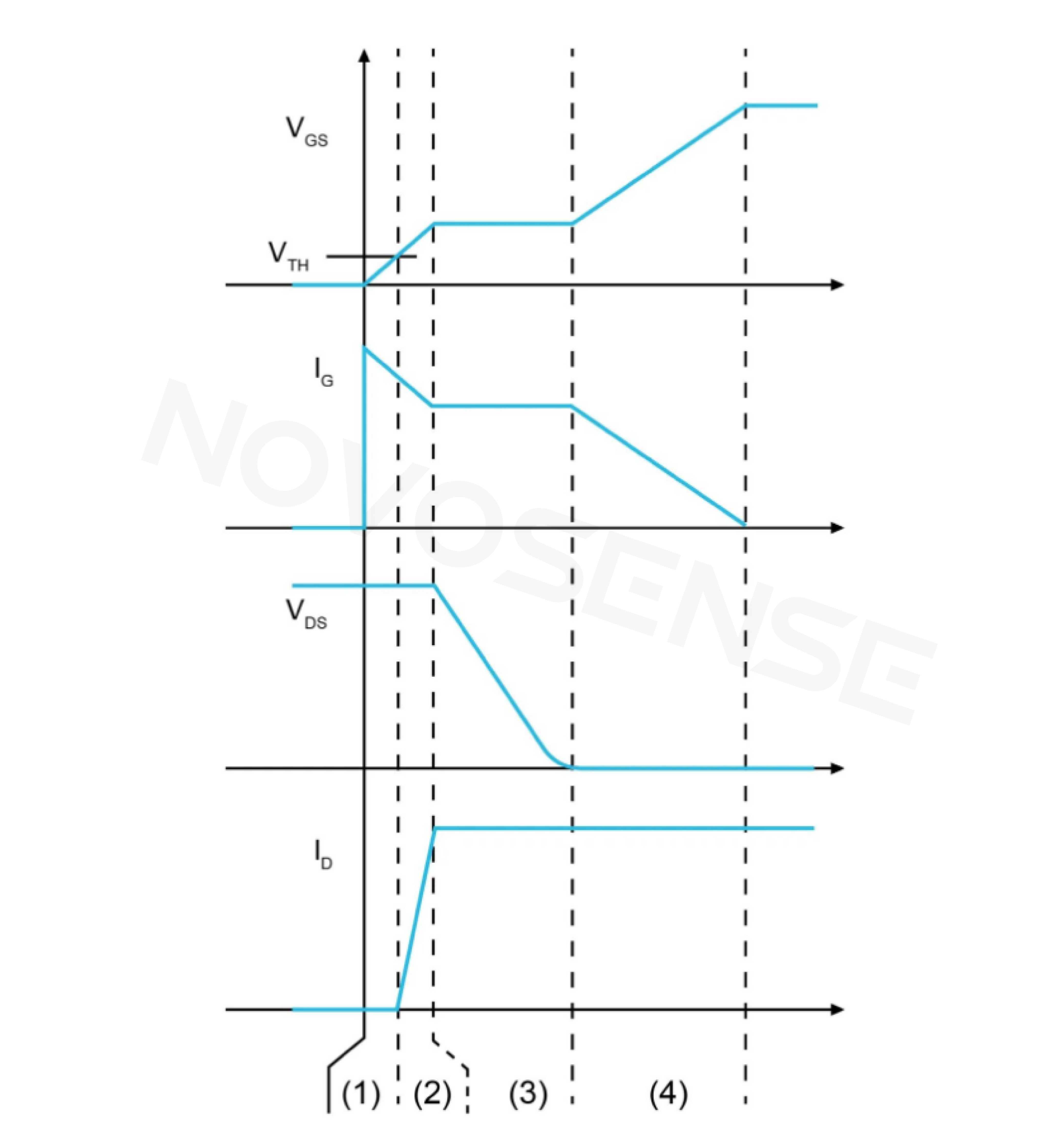
Figure 3
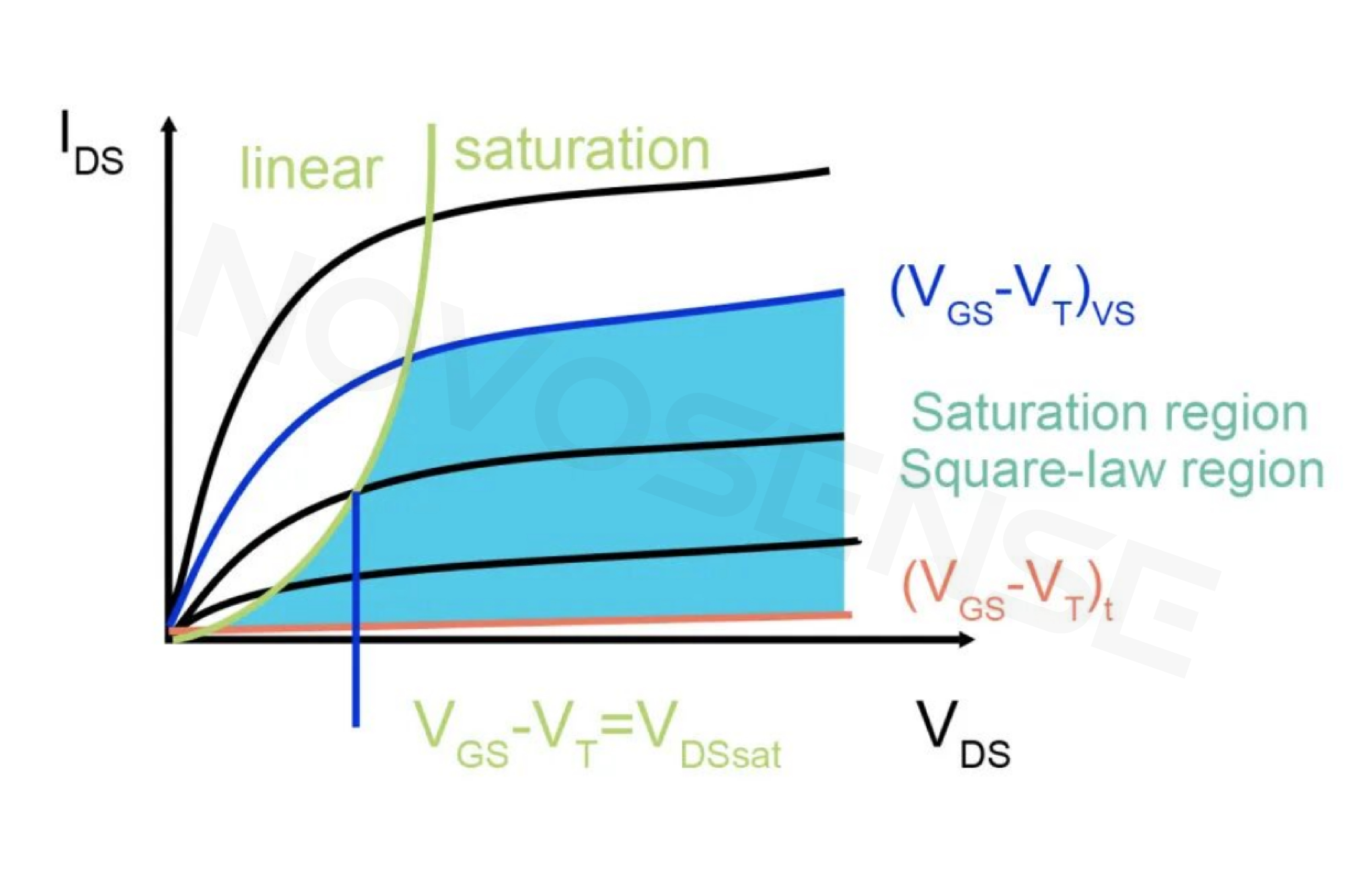
Figure 4
Stage (1): The MOSFET is in the cutoff region, where the capacitance is CGATE= CGS+CGD.
Stage (2): The MOSFET is in the saturation region, where the capacitance is CGATE=CGS+CGD*(1+gm*RLOAD).
Stage (3): The MOSFET is in the saturation region, where the capacitance is CGATE=CGD*(1+ gm*RLOAD).
Stage (4): The MOSFET is in the linear region, where the capacitance is CGATE=CGS+CGD.
CGS and CGD can be found in the MOSFET datasheet, where CISS= CGS+CGD, CRSS= CGD.
Due to the Miller effect in the saturation region, CGD is amplified by a factor of (1+AV/V), where AV/V represents the amplification factor of the MOSFET in the saturation region.
CGD varies with voltage. For most MOSFETs, the following approximation formula applies:
……（6）
At stages (1), (2), and (4), CISS can be approximated as CGS in parallel with CGD_AVG. At Stage (3), VGS remains nearly constant, rendering CGS ineffective, and the driver charges CGD with a constant current.
(1) Power loss during constant-current charging in stage (3) of Figure 3
Energy dissipated in resistor
……(4)
Energy stored in capacitor 
……(5)
When VDRV-Vmiller=Vmiller, Vmiller=VDRV/2, the energy dissipated in the resistor equals the energy stored in the capacitor. When VDRV>2Vmiller, the resistor dissipates more energy than the capacitor stores.
Energy supplied by the source ES=VDRV*IG*t=CGD*VDRV*VDS_off=ER+EC……（6）
(2) Power loss in RC charging (Stages (1), (2), and (4) of Figure 3 combined)
Let CG=CGS+CGD_AVG; voltage of CG at the end of charging UO=k*UDRV; charging duration is T; charging current is IG:
Energy stored in capacitor
……(7)
Energy dissipated in
resistor
……(8)
, indicating that the energy stored in the capacitor is always less than
the energy dissipated in the resistor. As the capacitor approaches full charge,
the two values become closer.
Energy supplied by the source
……（9）
3.Capacitor Charging of MOSFET
In real-world circuits, when a driver IC charges the MOSFET, most of the
charging current is supplied by a capacitor, allowing the driver circuit to be
approximated as a model of capacitor-to-capacitor charging.
(1) Power loss
during constant-current charging in stage (3) of Figure 3
Energy dissipated in resistor ER=CGD*VDS_off * (VDRV_AVG - Vmiller)
Energy stored in capacitor EC=CGD*Vmiller*VDS_off
Energy supplied by the
source capacitor ES=CGD*VDRV_AVG*VDS_off=EC+ER
Compared to the formula for constant voltage source charging capacitor, VDRV is replaced by VDRV_AVG,
because the source capacitor voltage decreases during charging, so the
average value over the charging process is used.
(2) Power Loss in RC Charging (Stages 1, 2, and 4 of Figure 3 Combined)
Let the initial voltage of the source capacitor CIN be UDRV, its instantaneous voltage be UIN; gate capacitance CG=CGS+CGD_AVG; voltage of CG at the end of charging UO=k*UDRV; charging duration is T; charging current is IG. As shown in Figure 5, voltage and current are solved using the s-domain model:
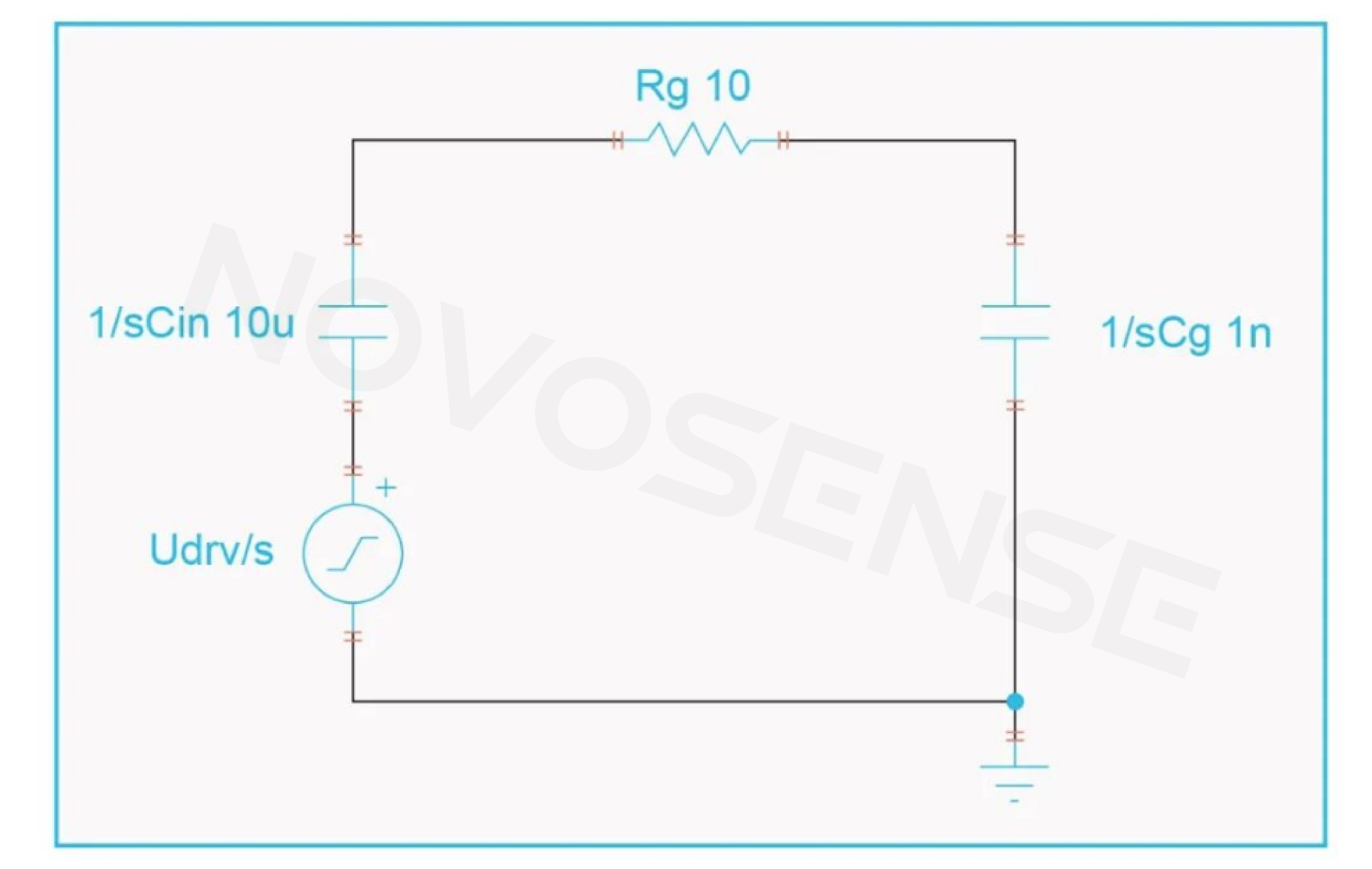
Figure 5
Let
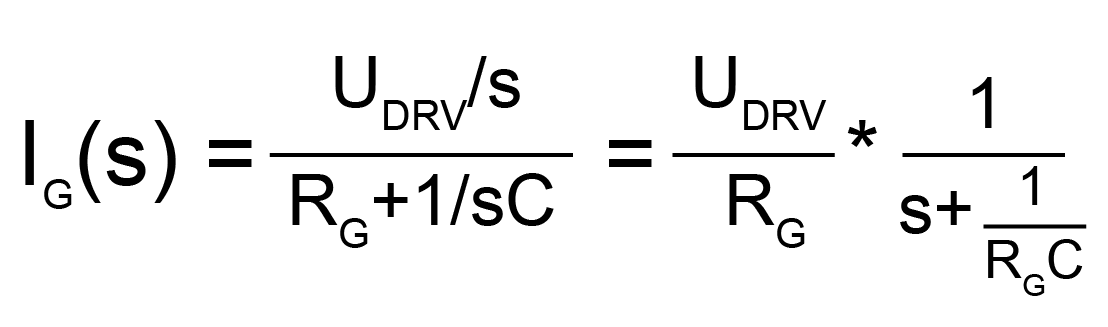
After inverse Laplace transform:
Energy stored in capacitor
Energy dissipated in resistor
……(11)
Energy supplied by the source capacitor
When 
, 
meaning that the energy stored in the capacitor exceeds the energy dissipated in the resistor.
When
, 
meaning the resistor dissipates more energy than the capacitor stores.
……(13)
Let
……(14)
Assuming that at the end of charging, the voltages across the two capacitors are equal, charge conservation indicates:
, solving yiedls 
, substituting into Equation (14):
Equation (15) shows that the energy supplied by the source capacitor
exceeds the sum of the energy dissipated in the resistor and stored in the
capacitor.
When 
, i.e., CG=CIN, the denominator reaches its
minimum, and the greater the difference between capacitance values, the smaller
the energy loss.
4.Discharging of MOSFET
Let the initial capacitor voltage be UG, voltage at the end of discharging UO=kUG; discharge duration is T:
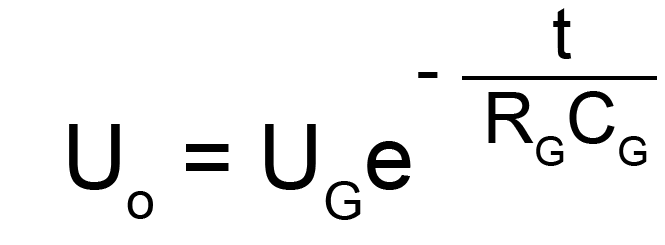
Remaining energy stored in capacitor
Energy dissipated in resistor
Initial energy stored in capacitor
Therefore, during discharge, the energy released by the capacitor is entirely dissipated in the resistor.
5.Effect of Parasitic Inductance
The charging loop acts like a single-turn coil, introducing parasitic inductance. The model in Figure 6 more closely resembles real-world circuits.
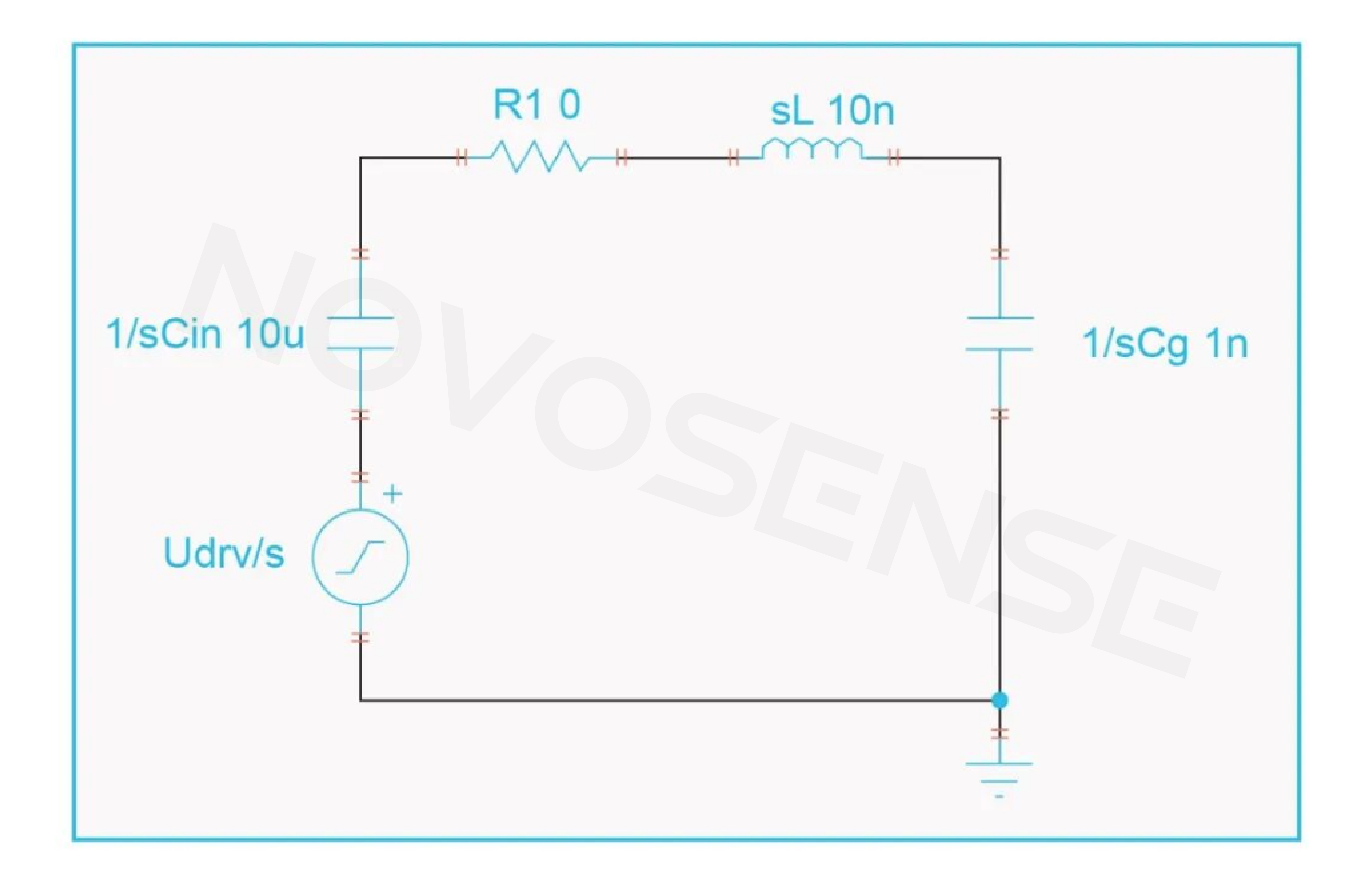
Figure 6
In Stage (3) of Figure 3, which approximates constant-current charging,
the effect of inductance is negligible and thus not analyzed.
Let the initial voltage of the source capacitor CIN be UDRV, and its instantaneous voltage be UIN; gate capacitance CG=CGS+CGD_AVG; voltage of CG at the end of charging UO=k*UDRV; charging duration is T; charging current is IG; parasitic inductance is L; 
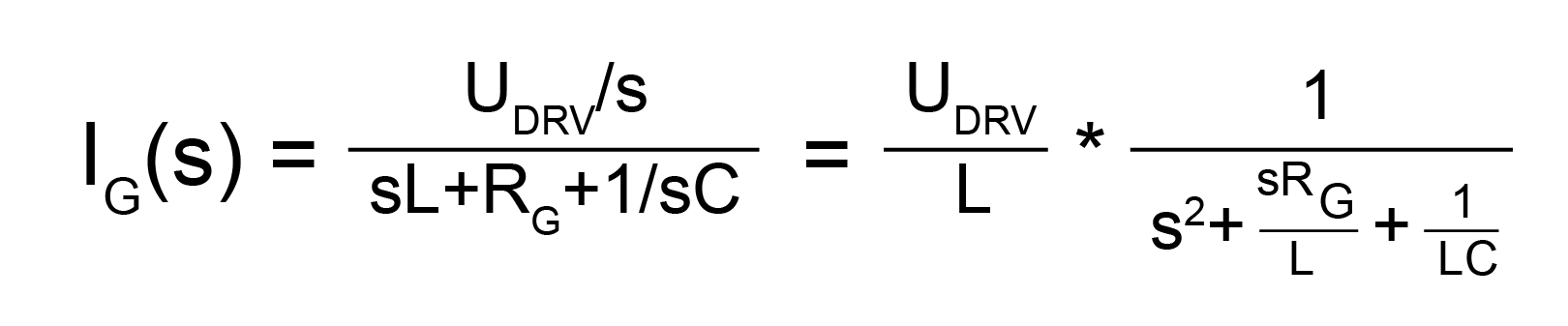
Since the time-domain expressions for IG and UO are extremely complex, T cannot
be derived, nor can the resistor’s energy dissipation be calculated via
formula. Since the resistor merely dissipates part of the energy, setting the
resistance to zero simplifies the analysis, leaving only L and C in the
circuit.
， 
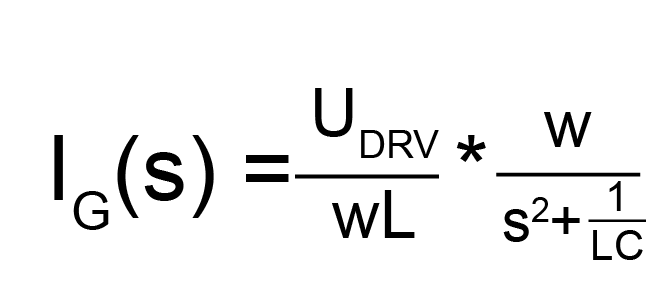
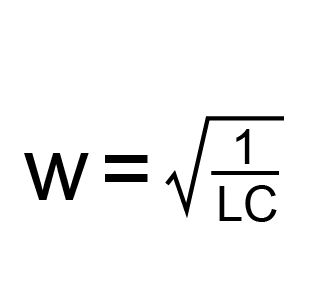
After inverse Laplace transform:
Energy stored in inductor at any time
…… (16)
Energy stored in MOS capacitor at any time
…… (17)
Energy stored in source capacitor at any time
…… (18)
Initial energy stored in source capacitor
……(19)
Equation (19) confirms energy conservation, with no additional energy loss. Of course, alternating electromagnetic fields will still radiate energy, but the presence of inductance suppresses the rate of current change.
6. Summary
Through quantitative analysis of the relationships among the energy dissipated in resistor, the energy stored in capacitor, and the energy supplied by the source under different charging models, this article demonstrates that the traditional assumption of “50-50 energy split” does not always hold. Particularly when the drive voltage exceeds twice the Miller level, energy dissipation in the gate resistor often exceeds the energy stored in the capacitor. In the capacitor-to-capacitor charging model, the energy distribution exhibits different characteristics. Additionally, during MOSFET turn-off, all stored energy is dissipated through the resistor, while parasitic inductance helps suppress energy loss to some extent. Understanding these energy paths is crucial for the precise design of high-efficiency gate driver systems, especially in high-frequency, high-density, and high-reliability power applications.
NOVOSENSE NSI67x0 series smart isolated drivers are
suitable for driving power devices such as SiC, IGBTs, and MOSFETs, and are available
in both automotive (AEC-Q100 compliant) and industrial variants. This product
series is widely used in new energy vehicles, air conditioners, power supplies,
photovoltaics, and other applications. Samples of the NSI67x0 series are now
available. Scan the QR code above to complete the questionnaire for sample
requests. For further inquiries, please contact sales@novosns.com. For more
product information and technical data, visit www.novosns.com
.
